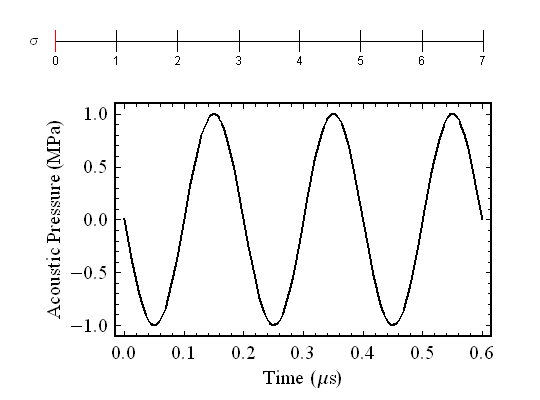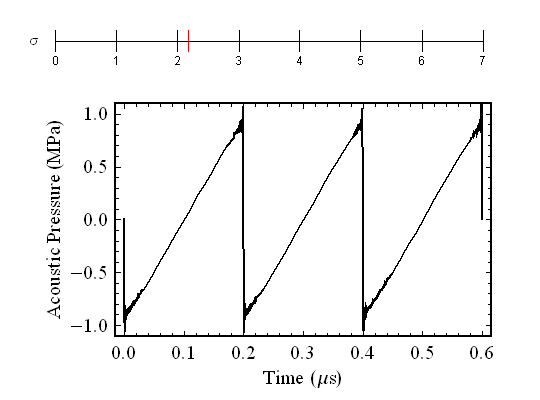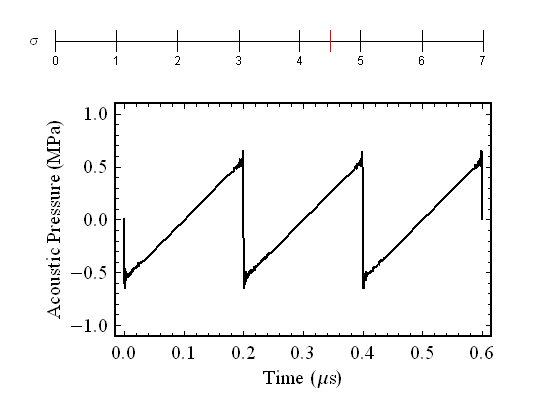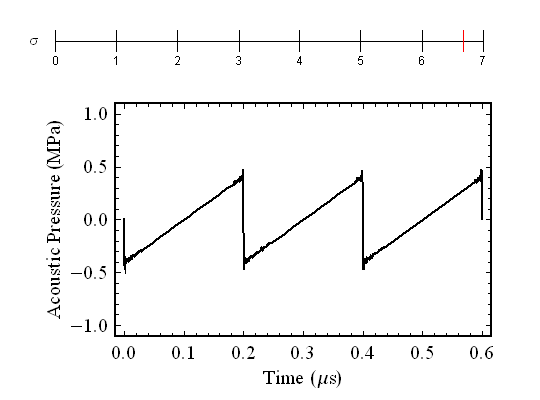
The term "nonlinear" is applied to many aspects of physics. In the case of sound propagation, it refers to the influence of several terms that are usually ignored in "basic" sound propagation. The basic equation is derived by assuming that the amplitude of the wave is infinitesimal. The major effect of nonlinear propagation is the conversion of a sinusoidal wave into a sawtooth, as shown in the following animated image.

To understand this figure, imaging that you are traveling along with the ultrasound source as it leaves the sound source (a transducer). As you travel with the wave, you are able to examine the pressure distribution in the wave. The tickmarks at the top of the figure indicate your relative distance from the source. Areas of the wave where the pressure is larger than zero (called compressional zones) travel slightly faster than those areas near zero amplitude. The opposite happens with the areas of the wave with smaller amplitude (also called rarefactional zones), they travel slower than areas near zero amplitude.
The cumulative effect of this is that the compressional zones starts to overtake the rarefactional zones. The pressure cannot be two numbers at once, so when they begin to meet, a discontinuity forms. In the figure the tickmarks at the top represent distance from the source relative to the distance at which this discontinuity first forms. Once the discontinuity forms, the amplitude of the wave begins to decrease as the resulting shock wave loses energy to its surroundings. The small wiggles at the corners are an artifact due to the method used to construct this image. If you have studied Fourier series, you should have heard about "Gibbs ringing", which is exactly what is happening at these locations.